200以上 二次関数 y=x2乗 グラフ 184843
Edu City Fukuyama Hiroshima Jp
26/1/19 二次関数y=x^2mxm3のグラフとx軸の正の部分が、異なる2点で交わる時、定数mのあたいの範囲を求めよ。の問題の解き方が分かりません。解説を入れてくださると助かります。お願いします。「Y=x²mxm3 のグラフが x 軸の正の部分で 2点Aを定数とし、xの2次関数y=x2乗2(a2)xa2乗a1のグラフをGとする。 を埋める問題です。 （1）グラフGとy軸との交点のy座標をYとする。Yの値が最小になるのは 質問＜2562＞さや「文字の入った2次関数の最大・最小」
二次関数 y=x2乗 グラフ
二次関数 y=x2乗 グラフ-定義：2次同次関数 、2次形式 ・「2変数x,yについての二次形式」「x,yの2次同次関数」とは、 2変数x,yについての多項式で、2次の項ばかりからなるもの すなわち、 Q (x,y) = ax 2 2 bxy c y 2 (a,b,cは定数) のことをいう。 ※詳細→2変数2次形式 文献2次関数のグラフ (3) §1 2次関数 4．2次関数のグラフ (3) この章では，一般形で表された2次関数のグラフを標準形に変形し，頂点と軸を求め，グラフを書くことにしましょう。 その前に，グラフを書くときのルールを説明しておきます。 ルールⅠ 座標軸 x,y
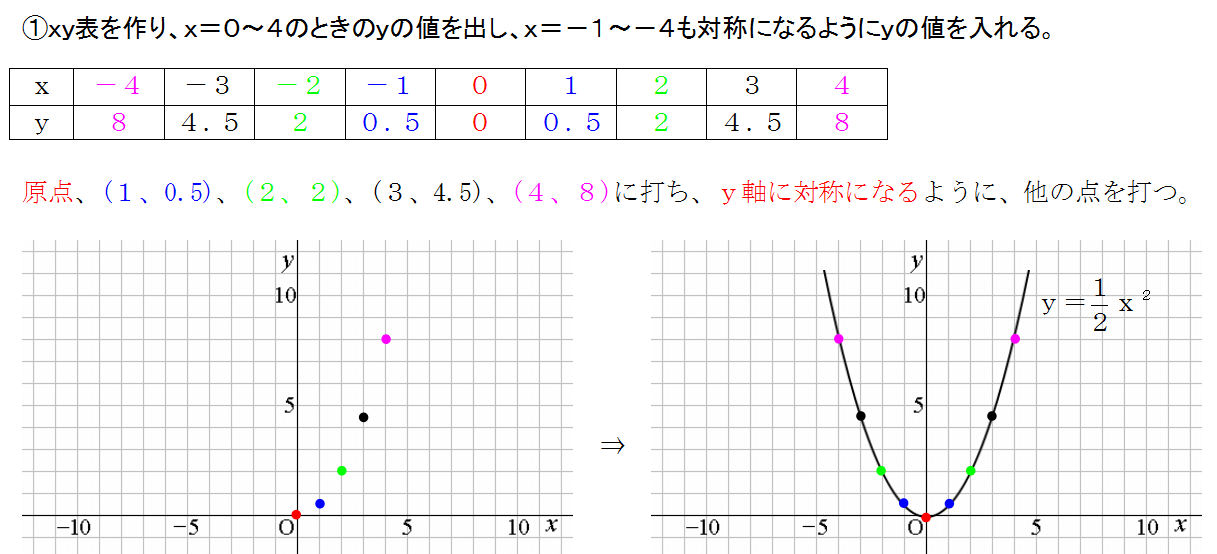
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
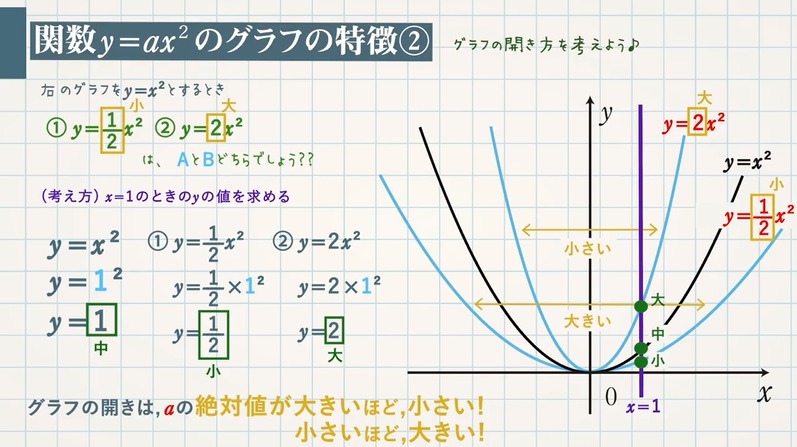
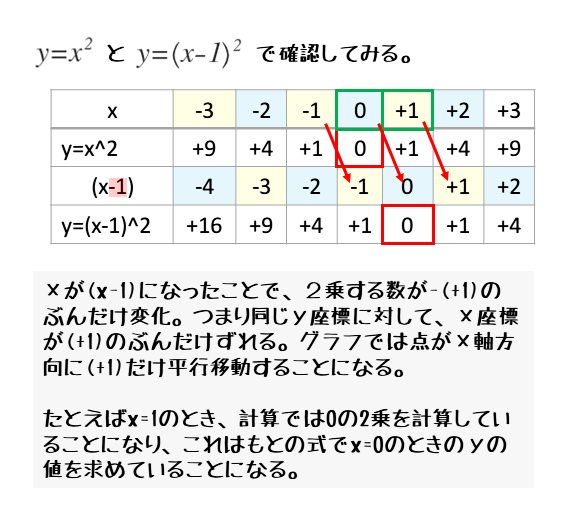
中3数学。2乗に比例する関数 (y ＝ ax²)。この a は「変化の割合」？ xの値が「0から2まで」増加する？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ 2次関数のコツ、成績アップ法を公開。A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 A(2,1), B(2,8) A(4, 4), B(4, 8) A(3, 1), B(3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標がY = f (x) y = f ( x) のグラフを、 x x 軸方向に p p y y 軸方向に q q 平行移動すると、 y− q = f (x− p) y − q = f ( x − p) になる。 これは、 2 2 次関数以外のあらゆる関数に成り立つことです。 今後も様々なところで出会うことになるでしょう。 なぜこれが
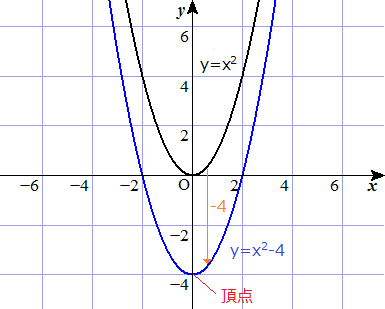
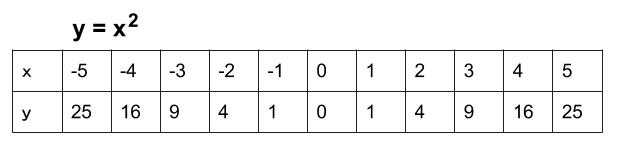
右図のように2次関数 y=x 2 のグラフと直線 y=x2 のグラフが x 軸， y 軸と交わる点をそれぞれ D ， C とするとき，次の問いに答えなさい． (1) 点 C ， D の座標を求めなさい． (2) 点 P は2次関数 y=x 2 のグラフ上で x y=x^22x3の平方完成について(x^22x)3(x1)^24となったのですがなぜ頂点は（1,4）ではなく(1,4)になるのでしょうか？(x1)^2 の項は x=1のとき0、x≠1のとき負は明らかですよね。つまり、(x1)^24 が最も大きなるのは X=1のと二次関数のグラフ③ のグラフについて考えてみよう。 について考えよう。 な滑らかな曲線になるんだ。 ↓曲線になるまで画像をクリック！ 値の 2 倍になっていることがわかるかな？ これは表からも明らかだね。 2倍だね！
二次関数 y=x2乗 グラフのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 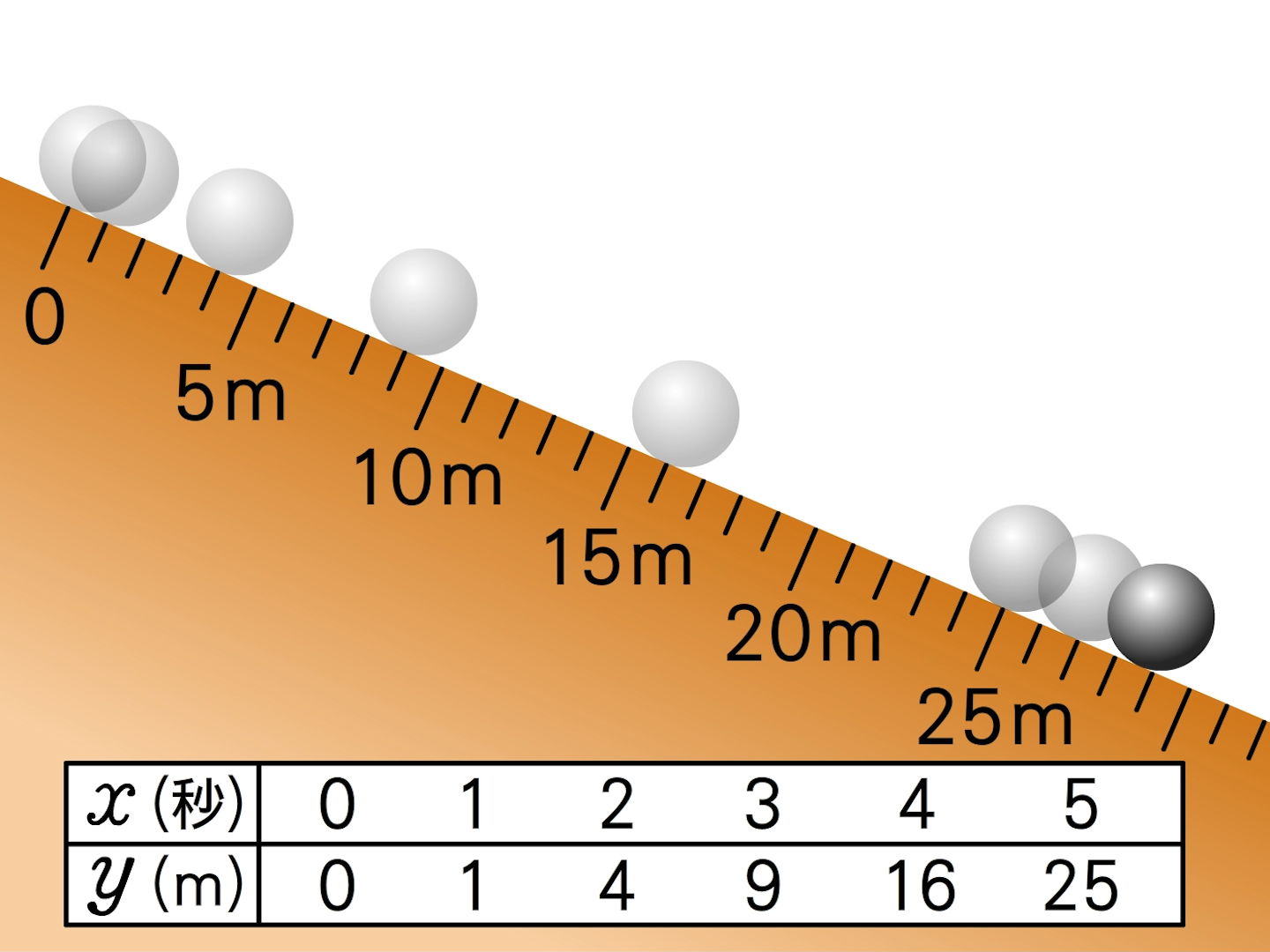 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 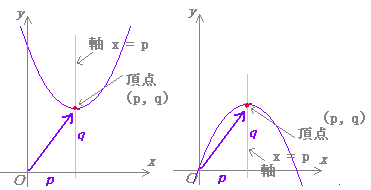 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
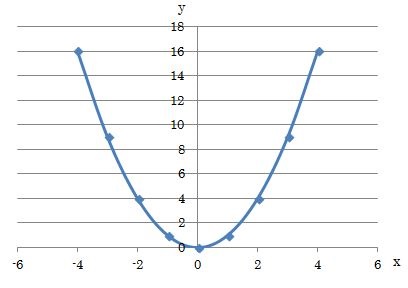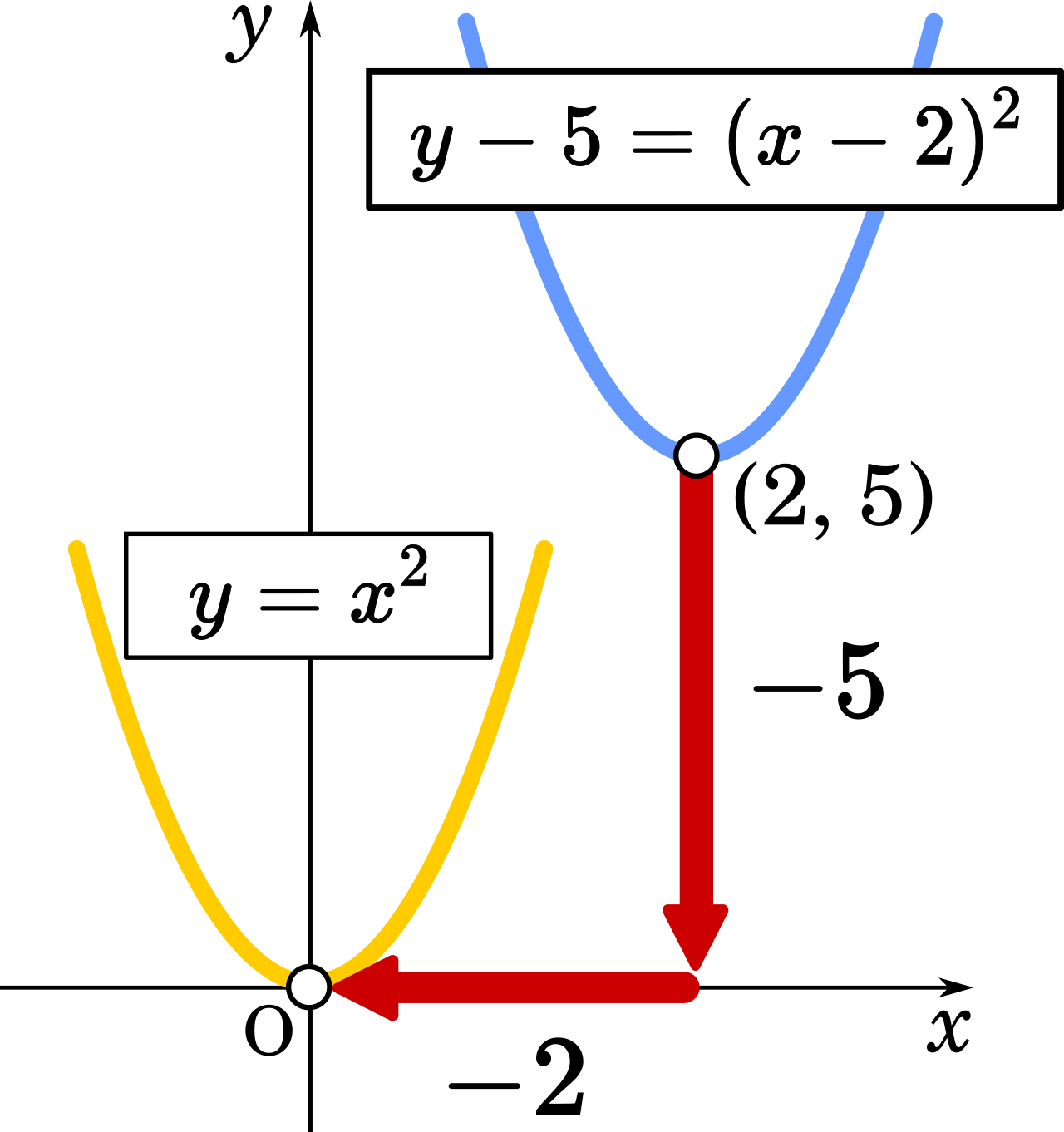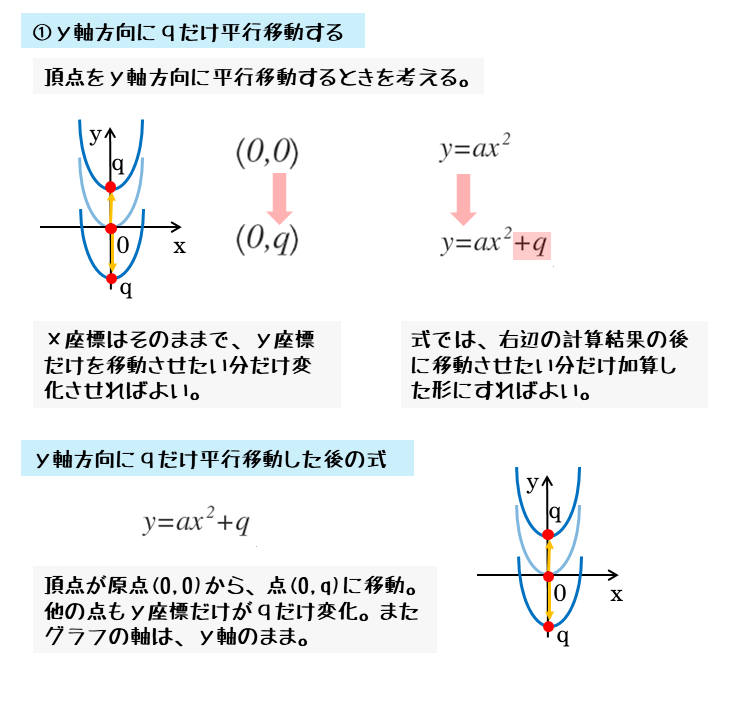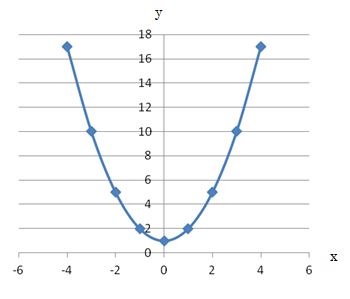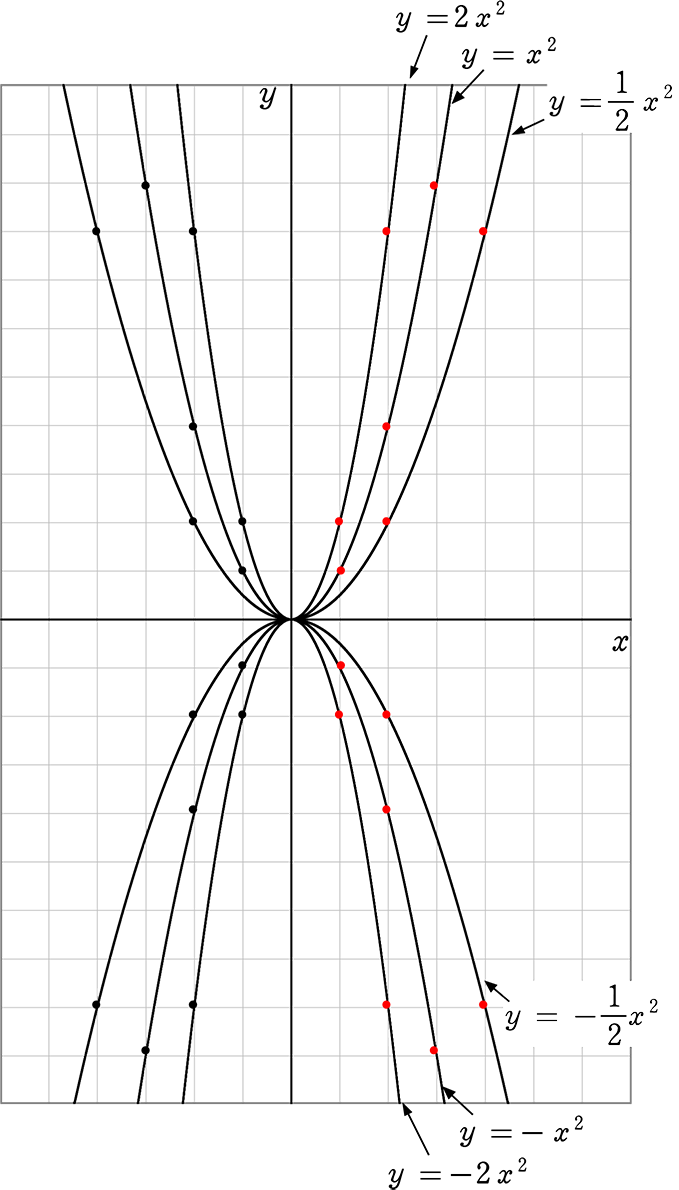 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |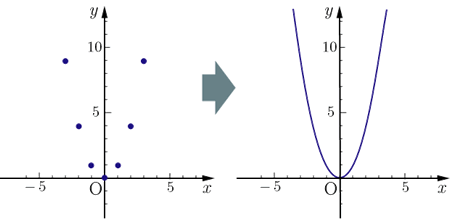
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 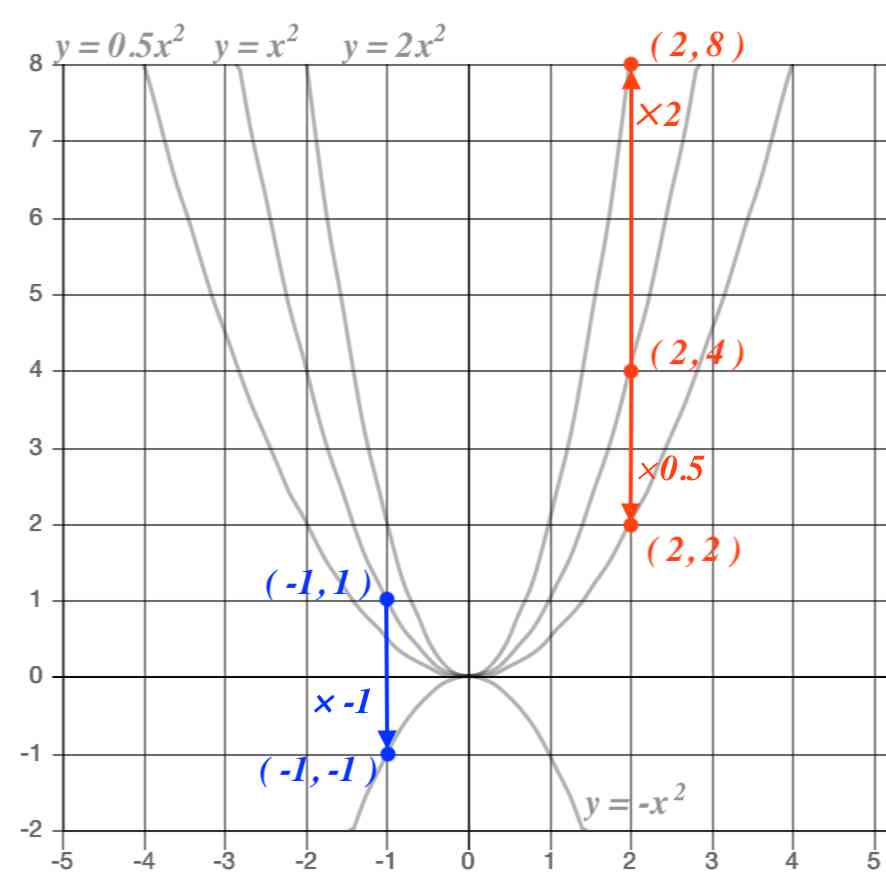 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
「二次関数 y=x2乗 グラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 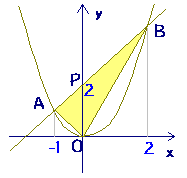 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |  2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 | 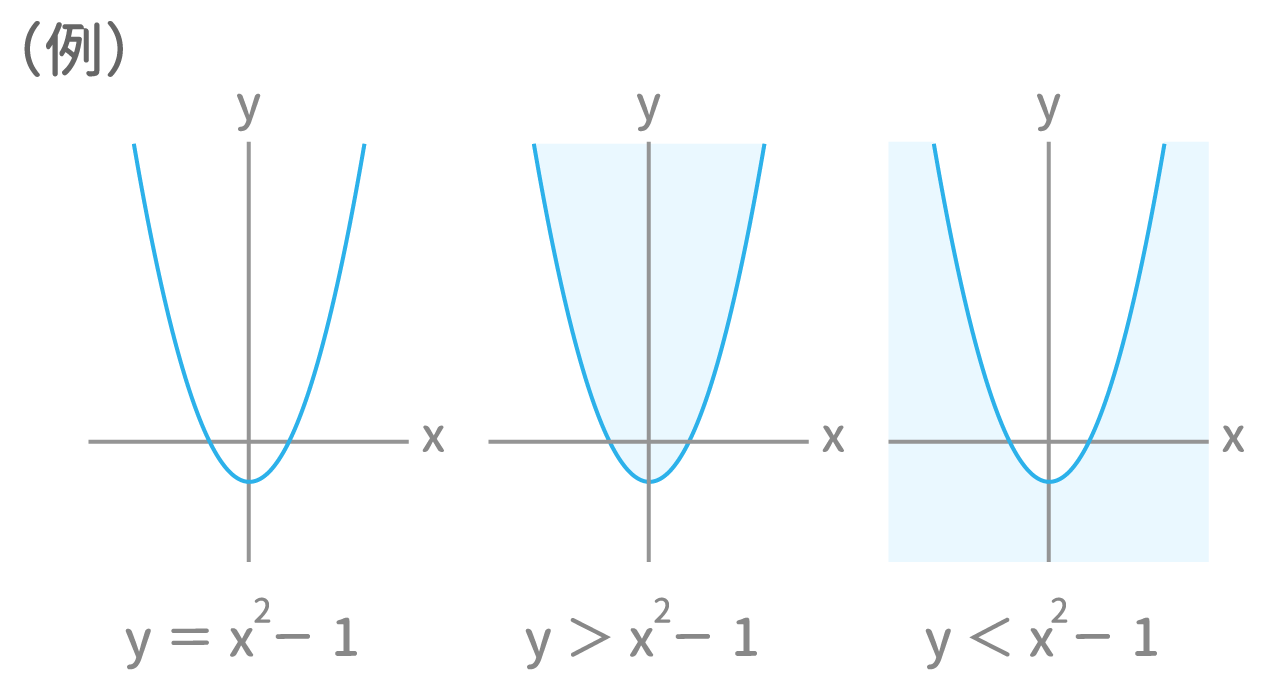 2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題 |
二次関数の平行移動・対称移動に関する問題は、 二次関数の頂点の移動に着目して ` y = a(xp)^2 q ` に代入して解く方法と、平行移動の公式、対称移動の公式に代入する方法があるよ。 公式を使った方が速いし、計算ミスも少なくなるので、ぜひ公式をマスターしよう。8/1/19 さて、二次関数の存在範囲や係数決定問題でほぼ必ず確認するのは以下の点です。 （逆に、これ以外に見るポイントはほとんどありません) ・判別式Dとx軸との交点 ・グラフが上に凸（うえにとつ）か下に凸か ・軸と頂点の座標 ・x＝0、つまりy軸や、y軸
コメント
コメントを投稿